マンデルブロ集合などでよく使われるカラーリングのアルゴリズムにOrbit trapと呼ばれる手法があります.以前から試してみたかったのですが,ようやくある程度理解でき,このような作品をつくることができました.

Kleinyan Cat at Shadertoy
今考えるとたいした事はないアルゴリズムだったのですが,割と理解するのに時間がかかったのでまとめておきます.やはり,実際に手で書いて試してみるのが大事ですね…
Orbit trapとマンデルブロ集合
マンデルブロ集合のようなフラクタルは,Escape-time Fractalとも呼ばれ,ある式を繰り返し計算していき,その計算結果の収束,発散をみることで描かれるフラクタルです.
マンデルブロ集合の計算の仕方を簡単にまとめると,複素平面上に格子点を取ってその座標を複素数Cとし,以下の漸化式を繰り返し計算します.
が無限大に発散しないものがマンデルブロ集合となります.また,
となると無限大に発散することがわかっています.
複素平面上の複素数の積は点の回転,拡大,縮小,複素数の和は点の平行移動になりますので,複素平面上に点の軌道が描かれることがわかります.
この軌道上にtrapとなる図形などを設定しておき,そこからの距離や角度を保持して,これを用いてカラーリングを行います.
点を用いたOrbit trap
まずは最も簡単な点を用いたOrbit trapを見てみます.
private double getDistance(Complex c, Complex point, int maxIteration) { double distance = 1e20; Complex z = new Complex(0, 0); for(int i=0; i<maxIteration; i++) { //Perform Mandelbrot iteration z = z.multiply(z); z = z.add(c); //Set new distance dist = min( dist, |z-point| ) Complex zMinusPoint = new Complex(z); zMinusPoint = zMinusPoint.subtract(point); double zMinusPointModulus = zMinusPoint.magnitude(); if(zMinusPointModulus < distance) distance = zMinusPointModulus; } return distance; }Orbit trap - Wikipedia, the free encyclopedia
レンダリング結果は載っていませんが,アルゴリズムの概要をWikipediaから引用しました.こうしてみると単純ですね.点を用いたOrbit trapで,あらかじめ設定した点と最も近い時の距離を用いてレンダリングを色を決定します.これとほぼ同じアルゴリズムで(-0.5, 2.0)の点でトラップし,distanceをそのままプロットしたのが以下の画像です.この画像はShadertoyのMandelbrot - orbit trapsを少し変更して生成したものです.

黒い点が連なっています.マンデルブロ集合では点の軌道がわかりにくく,点が連なる理由が見えてきません.個人的になれている接触ショットキー群でも考えてみたいと思います.
Orbit trapと接触ショットキー群

4つの円で構成される接触ショットキー群を考えます.この画像は,マンデルブロ集合と同じように,複素平面上に格子点を取り,その座標が4つの基本となる円盤に載っていた場合にその円に関する鏡映反転を行う,という操作を点がすべての円の外に出るまで繰り返し,その繰り返した回数に応じて色を塗った画像です.この点にも軌道ができますので,Orbit trapを行うことができます.
Kleinyan Catの191行目あたりのコメントアウトを外してCompileし直すと,次のような画像が得られます.
vec3 hsv = hsv2rgb(vec3(0.04 * loopNum,1.0,1.0)); col.xyz = mix( hsv, col.xyz, col.w ); fragColor = col; if(trap1/1000. < 0.8){ fragColor = vec4(vec3(trap1/1000.), 1.0); }else{ fragColor = vec4( hsv, 1.0); }
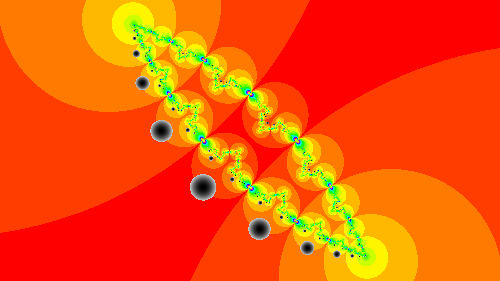
これはt1c = vec2(-100, -100)と軌道の点が最も近い時の距離を保持し,スケーリングしてプロットしたものです.パラメータが動いても動かない点がありますが,これが最初に設定した点(-100, -100)です.
二つの円盤に点がかぶってしまっているのであまりよくない画像ですが,この図形の点の大体の軌道を考えてみるとこんな感じになると思います.
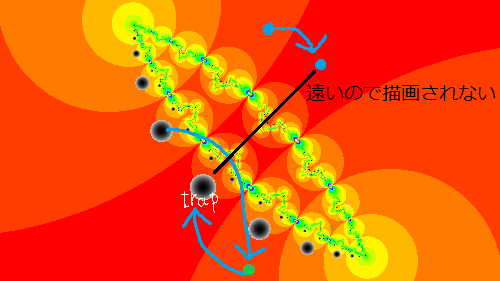
それぞれの点は反転を行うと,円の中心から点の方向に,円盤ひとつずつ降りていくような挙動を取ります.トラップする点,t1cを弄ってみるとより点列ができる理由がわかりやすいかもしれません.
ちなみにこの図形は二つの領域に円の極限(極限集合)で分けられており,この内側の点は内側に,外側の点は必ず外側に移るようになっています.つまり,内側にトラップする点を置いておくと,点列は内側にしか現れません.t1cを(0, 0)に置いてみるとよくわかります.

Orbit trapを用いたカラーリング
アルゴリズムは案外単純であることがわかりましたが,果たしてこれで面白いカラーリングができるのでしょうか…iq先生のMandelbrot - orbit trapsでは点との距離を見るトラップとaverage trap distance to lineというトラップを行い,それらをうまく変換しているようです.ズームや,経過時間に応じてトラップする点をずらすなど,色々とうまくやっているようで,使いこなすには経験とセンスが必要な気がします…定石などがあるのでしょうか.
今回はlineに関するtrapは試していませんが,64行目あたりの
col += 2.0*sqrt(c1*col1*col2);
を
col += c2;
にすると大体の挙動がわかります.
Bitmap Orbit traps
さて,次にtrapに画像を用いるBitmap Orbit trapを行ってみたいと思います.こちらは絵を移していくものなので,普通に色付けするよりは簡単に面白いものができるのではないかと思います.Bitmap Orbit trapの実装はFractal Nyancatが参考になります.Kleinyan Catのトラップの処理は以下のようになります.
if (col.w < 0.1) col = getNyanCatColor( pos - cPos[0] * scale); if (col.w < 0.1) col = getNyanCatColor( pos - cPos[1] * scale); if (col.w < 0.1) col = getNyanCatColor( pos - cPos[2] * scale); if (col.w < 0.1) col = getNyanCatColor( pos - cPos[3] * scale);
cPos * scaleがトラップする点です.点の位置から引くことで画像の始点からの位置を求めています.画像は原点から四円の中心への直線の延長直線状に置いています.絵がない部分には,透明度が設定されているので,絵が取得されていれば画素値は取得されないようになっています.
getNyanCatColorという関数は,Fractal Nyancatで使われているものを整えました.
vec4 getNyanCatColor( vec2 p ){
p += vec2(100, 100);//offset
p = p / 200.;
p = clamp(p,0.0,1.0);
p.x = p.x*40.0/256.0;
float fr = floor( mod( 20.0*iGlobalTime, 6.0 ) );
p.x += fr*40.0/256.0;
return texture2D( iChannel0, p);
}
トラップに使用する点の中心に画像を置きたいので,適当に移動した後にスケーリングします.ここら辺は実験的に決めましたが,ちゃんと考えれば一般的な解はあるはずです.
clampすることで,0以下は0に,1以上は1に丸まられ,画像から離れすぎた場所は角の画素が参照されることになります.こうすることで,パフォーマンスに影響がでる条件分岐を削る事もできます.参照しているテクスチャは6フレームの猫が収められているので,うまく参照してやります.トラップに用いる最初の猫の位置はこのような感じです.(フレームの外側に2体隠れていて,合計4体描かれているはずです.)

点の軌道上に,最初に置いた猫の画像があれば,そこから画素値を取得し,その色を取得する感じです.結果としてこのような画像が得られました.

移された猫は隣り合う円盤同士で鏡写しになり,歪みが入っているのがわかるでしょうか.これが円に関する鏡映変換の作用です.また,この結果はクライン群を生成する4つの生成元で一つの画像を写していくことと同じようです.以前描いた以下のようなものが大元となる一体の蝶を4つの生成元で移したものです.
GitHub - soma-arc/KleinianWalker: Draw limit set of Kleinian group and orbit of figure
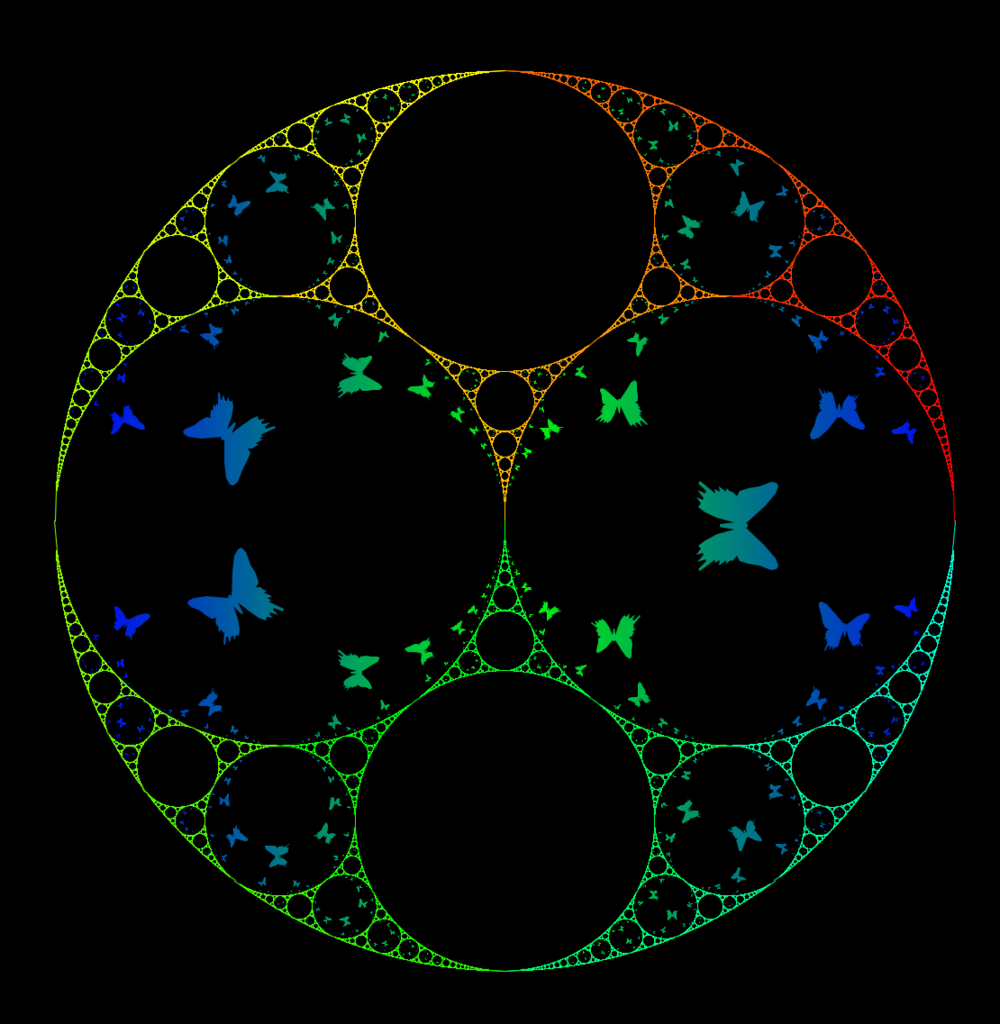
生成元で直接移していくためには,生成元の組み合わせの木構造を幅優先で探索していかなければならないのですが,探索が深くなるにつれて,指数オーダーで計算量が増えていくので,細かく描こうとするほど時間がかかります.Bitmap Orbit trapが使えれば,そのような探索が必要でなくなり,高速な描画ができるということになります.
おわりに
今回は点と画像を用いたOrbit trapのみを試しましたが,他の種類のものも試す必要がありますね.また,Bitmap Orbit trapを用いることである画像を生成元で移していくような作品も高速に描画できることがわかりました.このようなテクニックはまだまだあるようで,一つ一つ実際に実装して理解していく必要がありそうです.日々精進あるのみですね.