GLSLで描くCircle Inversion Fractals

qiita.com
GPUで暖を取りたい人のためのGLSL Advent Calendar 2016，25日目の記事です．

前回の記事で紹介した円の反転という操作を用いてフラクタルを描いてみます．
f:id:soma_arc:20161220183920p:plain
まずはこの画像のような４つの円板とその反転を考えます．それぞれの円の反転は自分以外の円板を自分の内側に移します．よって，それぞれの円の内側には３つの円が移され，１２個の円ができています．次に，ショットキー円の反転を新たに現れた小円にも適用することを繰り替えすと，以下のように円が入れ子状に続いていきます．
f:id:soma_arc:20161220184220p:plain
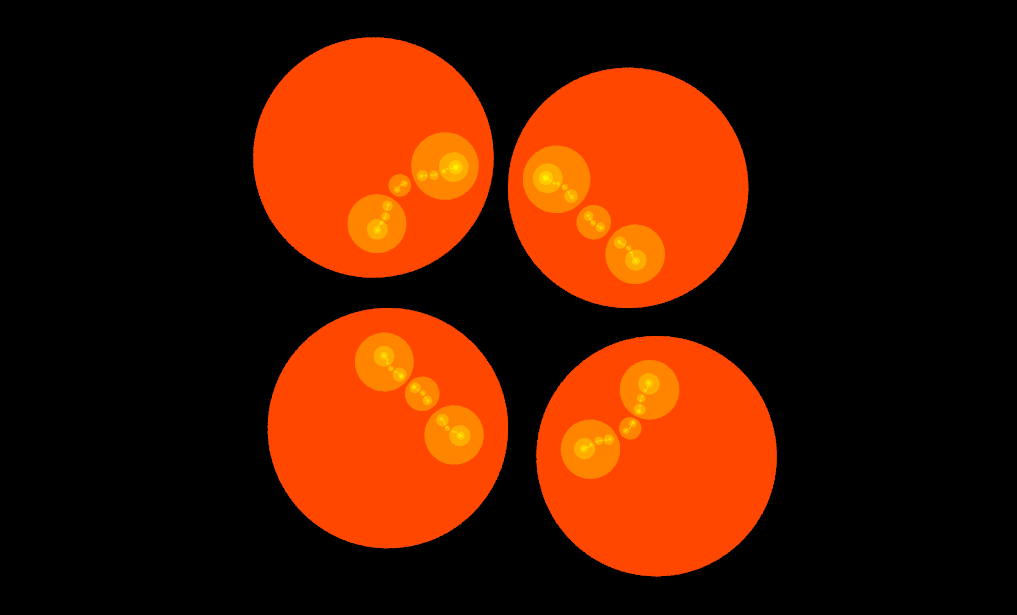
円が接するときには，このような美しいネックレス上の構造を見ることができます．これらの円列をショットキー円の軌道(Orbit)，円列の極限を極限集合と呼びます．
f:id:soma_arc:20161220184542p:plain
この処理はJavaScriptで書くと以下のような感じになります．

let orbits = [];
orbits.push(schottkyCircles); // level 0
for(let level = 1 ; level < MAX_LEVEL ; level++){
    orbits.push([]);
    for(let i = 0 ; i < orbits[level - 1].length ; i++){
        let orbitCircle = orbits[level-1][i];
        for(let j = 0 ; j < schottkyCircles.length ; j++){
            if(schottkyCircles[j].contains(orbitCircle)) continue;
            let nc = schottkyCircles[j].invert(orbitCircle);
            orbits[level].push(nc);
        }
    }
}
return orbits;

CPUで実装すると，変換の木構造を幅優先探索するようなコードになり，円の深さが深くなるに連れて指数オーダーで計算量が増えてしまいます．GLSLをつかったアプローチを用いると，非常に効率よく描くことができます．

アルゴリズム

全ての点に対して，その点がいずれかのショットキー円の内部に存在するときに，点を属しているショットキー円による反転で移します．この操作を変換された点がすべてのショットキー円の外側に落ちるまで続けます．最後に，反転の回数が円の深さになっているので，深さに応じて色付けを行います．このアルゴリズムはIterated Inversion System(IIS)と呼んでいます．
f:id:soma_arc:20161223174333p:plain
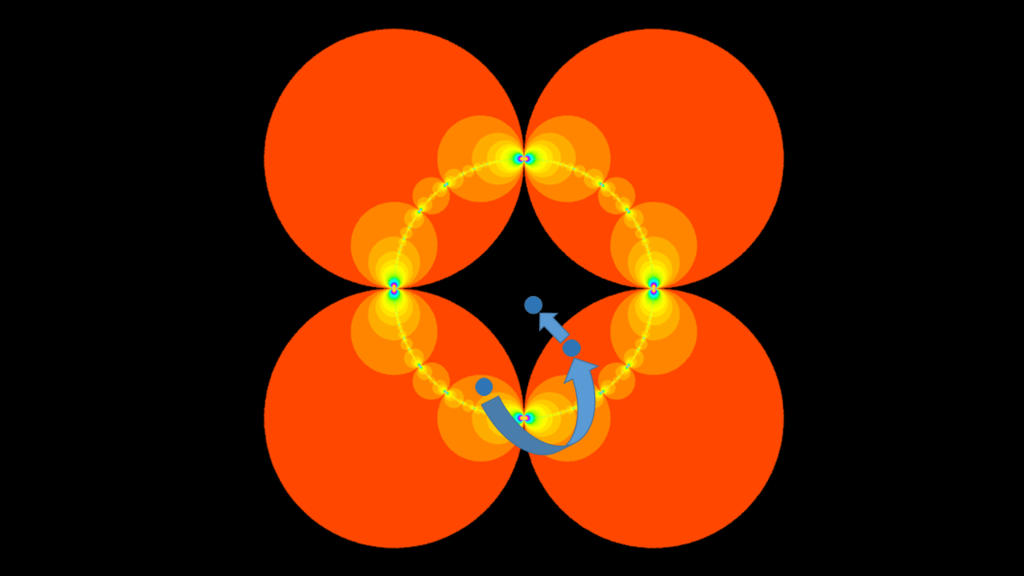
このアルゴリズムのコードを以下に示します．

const int ITERATIONS = 30;
int IIS(vec2 pos){
    int loopNum = 0;
    bool loopEnd = true;
    for(int i = 0 ; i < ITERATIONS ; i++){
        loopEnd = true;
        if(distance(pos, c1Pos) < c1Radius){
            pos = circleInvert(pos, c1Pos, c1Radius);
            loopEnd = false;
            loopNum++;
        }else if(distance(pos, c2Pos) < c2Radius){
            pos = circleInvert(pos, c2Pos, c2Radius);
            loopEnd = false;
            loopNum++;
        }else if(distance(pos, c3Pos) < c3Radius){
            pos = circleInvert(pos, c3Pos, c3Radius);
            loopEnd = false;
            loopNum++;
        }else if(distance(pos, c4Pos) < c4Radius){
            pos = circleInvert(pos, c4Pos, c4Radius);
            loopEnd = false;
            loopNum++;
        }
        if(loopEnd) break;
    }
    return loopNum;
}

お気づきかもしれませんが．よく見ると極限集合の内側と外側は黒い基本領域をショットキー円で変換して敷き詰めた形状としても見ることができます．数学的な理由によって，Hyperbolic Tessellationのように極限で内側と外側が分けられるため，最終的に落ちた点が内側か外側かを判定し，処理を切り替えることで，極限のエッジをレンダリングすることができます．
f:id:soma_arc:20161223174902p:plain
f:id:soma_arc:20161223174846p:plain
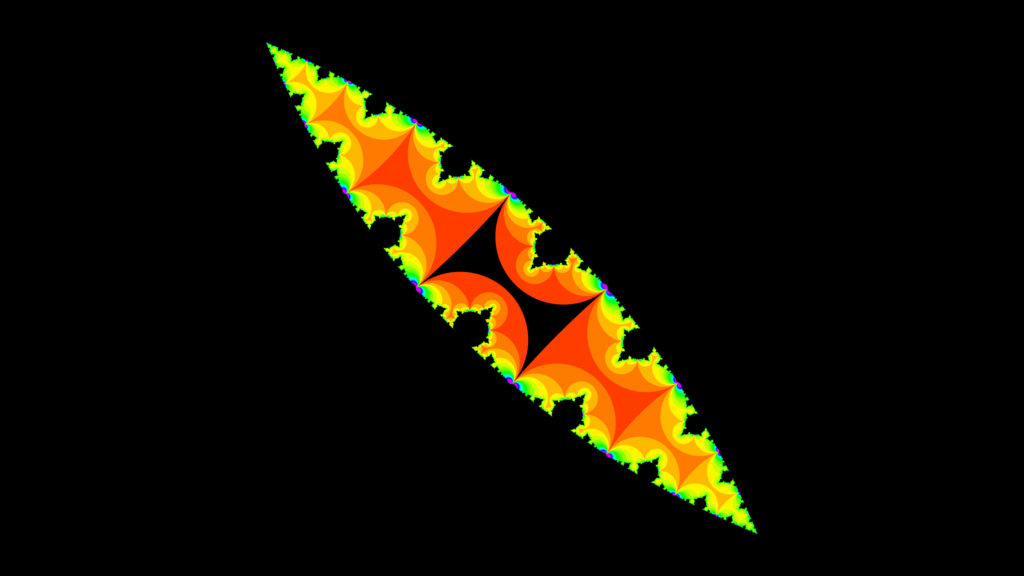
マンデルブロ集合に似たフラクタル状のエッジが綺麗ですね．
Kissing-schottky Limit set

Bitmap Orbit trapと組み合わせる

Bitmap Orbit trapという手法を用いるとテクスチャの軌道も描くことができます．ループの過程で，あらかじめ置いておいたテクスチャの領域に点が入った時に，テクスチャの色を参照してループを脱します．前々回の記事で猫を書いた時とほぼ同じ手法です．
f:id:soma_arc:20160421173008g:plain
このgifアニメは四か所に猫のテクスチャを配置しています．詳細はコードをご覧ください．
Kleinyan Cat
Bitmap Orbit trapは一年位前に書いた記事でもまとめておきました．
Orbit trapを考える - 心鏡曼荼羅
今読み返すと読みにくいので書き直したいところです…

三次元への拡張

このアルゴリズムを三次元に拡張し，球をベースにしたフラクタルを描くこともできます．今回はアドベントカレンダーの枠と時間がなく紹介することができなかったのでまたの機会に記事を書きたいと思います．興味のある方は僕の公開した論文，スライドやShadertoyのコード等を読んでみてください．
f:id:soma_arc:20161223181740p:plain

備考 - Schottky transformationについて

ショットキーという語はショットキー変換(Schottky transformation)から来ています．ショットキー変換は２つの円をペアとする変換で，相手の円板の外側を自分の内側に，自分の円板の外側を相手の円板の内側へと移す変換です．これは，本質的に円の反転と同じものになることがあります．ショットキー変換を構成する円のことをショットキー円と呼ぶのですが，奇数個の円を扱うことを考えると，厳密にはショットキー円とは呼べません．詳しくは，後述のインドラの真珠を読んでみてください．

おわりに

インタラクティブに円板を配置してフラクタルを描画することのできるWebアプリケーションを開発しています．また，単純な円盤以外の変換や，三次元のものも実装しています．
SchottkyLink
f:id:soma_arc:20161222215658p:plain f:id:soma_arc:20161223181515g:plain
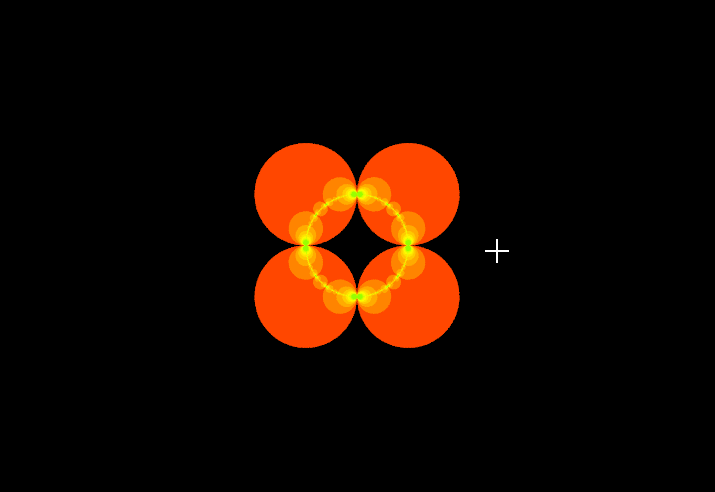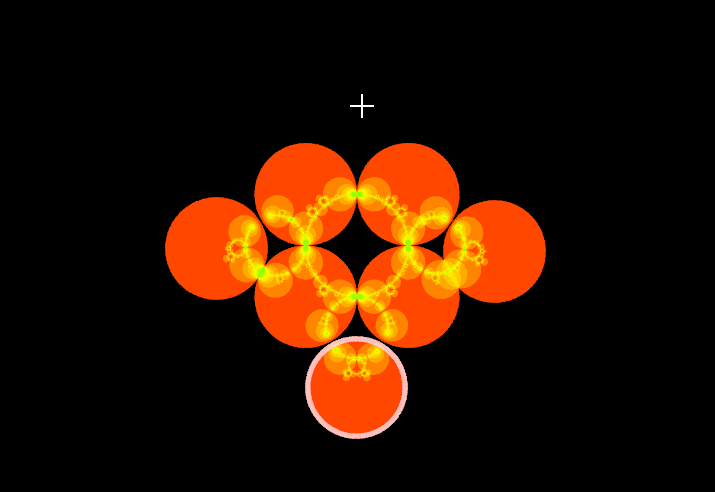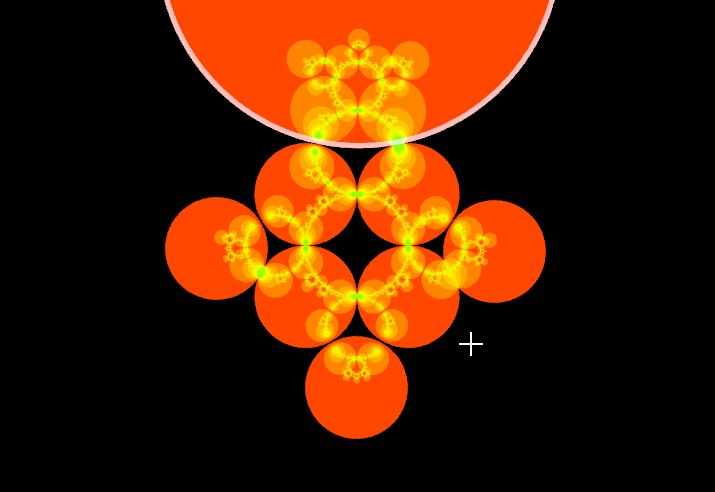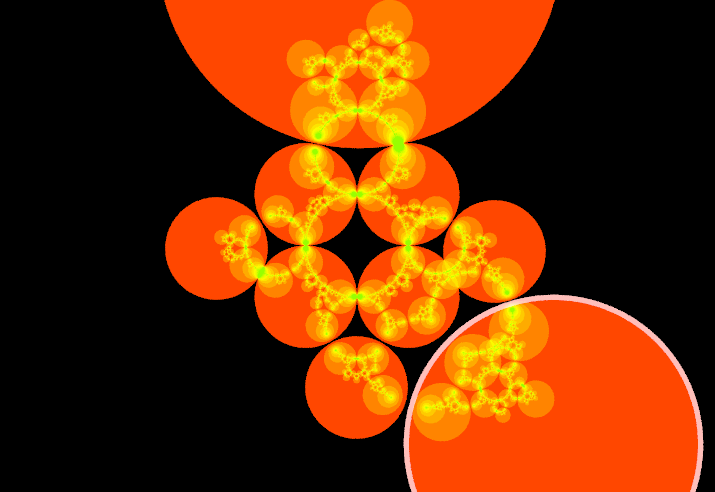
今回のGLSLアドベントカレンダーでは三回にわたって，Tessellationに関連するレンダリング手法を紹介しました．何かの参考になれば幸いです．それでは，来年の皆様のGLSLライフがより良きものになりますように．

アルゴリズム

Bitmap Orbit trapと組み合わせる

三次元への拡張

備考 - Schottky transformationについて

Further Reading

おわりに