GLSLで描くHyperbolic Tessellation

qiita.com
GPUで暖を取りたい人のためのGLSL Advent Calendar 2016，24日目の記事です．

前回の記事で紹介したアルゴリズムを用いて双曲円盤上での敷き詰め模様を描いてみます．前回の例では，ユークリッド平面，つまり私達が普段考える平面での敷き詰めを行いました．敷き詰め模様は無限に続き，果てが見えません．
幾何学を研究する数学者たちは，私達の世界の法則を崩した世界を考えました．双曲幾何学(Hyperbolic Geometry)はそんな世界を考える幾何学の分野の一つです．そして，双曲幾何学の世界を一枚の円盤だとみなしたモデルが存在します．このモデルはポアンカレの円板モデルと呼ばれ，円盤の端がユークリッド平面における無限遠点，世界の端となり，円弧がこの世界における直線だと考えられます．また，三角形の内角の和が180度以下になります．この世界におけるタイルの敷き詰めがHyperbolic Tessellationです．

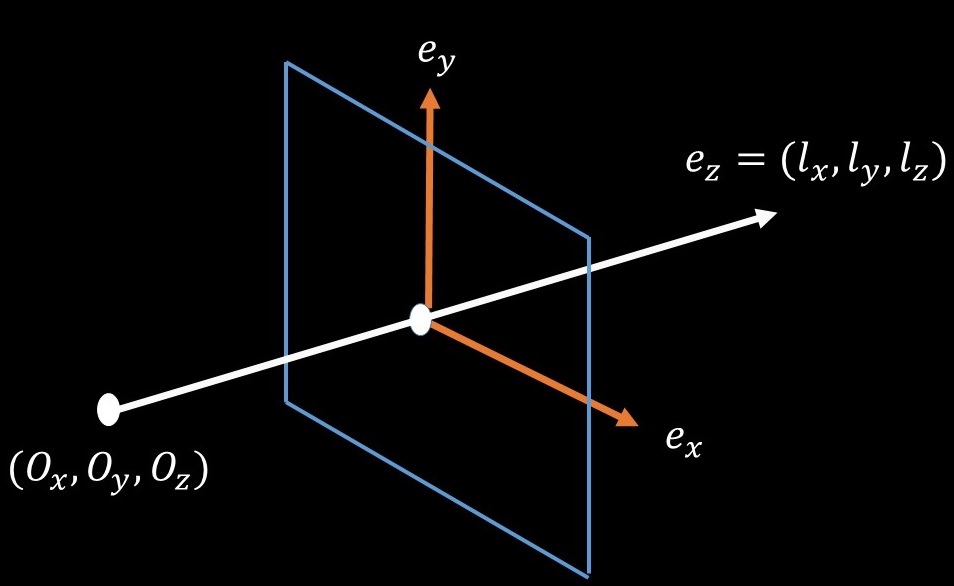
半球の内側にある円板がポアンカレの円板です．ユークリッド平面に対する双曲平面です．直線を半径が無限の円板の円周だとみなすと，あらゆるタイルが曲線で構成されていると考えることができます．円板の内側と外側は円板に関する反転という操作で移り合います．見た目は異なりますが，幾何学的，本質的な意味は変わりません．
画家のエッシャーはこのような敷き詰め模様に着想を得て，Circle Limitや天使と悪魔といった有名な作品を生み出しました．双曲幾何学や，Hyperbolic Tessellationに関して，厳密な話はここでは触れません．教科書等を参照してみてください．

基本タイルと変換を見つける

早速前回同様基本タイルを見つけていきましょう．

円板は原点中心，半径１の円とします．中央付近の一番大きなタイルがx軸，y軸と２つの円弧に囲まれているのがわかるでしょうか．Hyperbolic Tessellationでは円に関する反転という操作を使って敷き詰めを行います．今回はx軸対称，y軸対称，２つの円に関する反転をとり続けることで，この敷き詰めを描くことができます．

円の位置を特定する

Hyperbolic Tessellationは，タイルの辺の角度が重要になります．どんな図形でも敷き詰めることができるわけではなく，Hyperbolic Tessellationが成立する条件が存在します．これはポアンカレの貼り合わせ定理として知られています．例えば，双曲平面上での三角形である双曲三角形を考える場合は以下の条件を満たす必要があります．

以下の画像は一見正しそうに見えますが，正しい敷き詰めではありません．どこかでタイル同士が重なりあったりしています．

双曲四角形は２つの双曲三角形を貼り合わせることで得ることができます．今回のタイルは３つの角がPI/2，残りの角がPI/3の４辺形です．よって軸と垂直に交わり，円同士の角度がPI/3となる２円を求める必要があります．円の位置と角度の関係と双曲直線の条件から連立方程式を解きます．双曲直線の条件は以下の通りです．
円の中心を(x, y)半径をrとします．その円弧が双曲直線であるとき以下の条件を満たします．

今回の２円はだいたい中心(1.7317, 0),(0, 1.7317)半径はともに1.413となります．円の座標と半径を求める作業が一番面倒なのですが，時間ができたら他のタイルに関しても計算したいところです．

円に関する反転

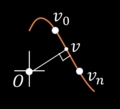
円に関する反転は，円の中心を無限遠点に，無限遠点を円の中心にもってくる操作です．この変換には等角性や円円対応といった面白い性質があります．ある点Pを中心C，半径Rの円で反転する式は以下のようになります．


円の外側に描いた図形を黒の円に関する反転によって変換するとこのような図になります．直線は円に，円は円に移ります．変換の前後で図形の角度は変わりませんが(例えば緑の四角形の内角は変換後も直角を保つ)，面積などは大きく変化します．また，同様にして三次元空間で球の反転を定義することもできます．

Hyperbolic Tessellationを描く

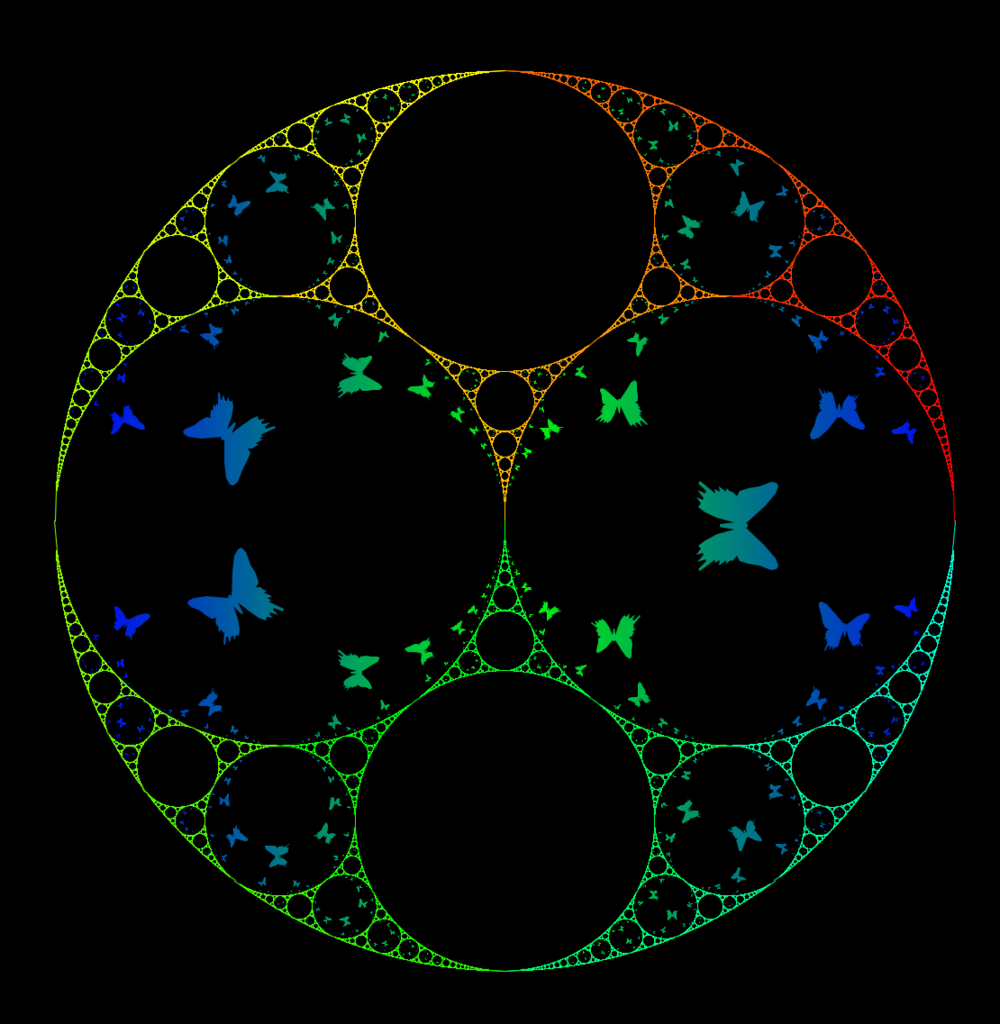
中央の一番大きな４つのタイルのうち，右上のタイルを基本タイルとした敷き詰めのコードが以下のようになります．

for(int i = 0 ; i < ITERATIONS ; i++){
    fund = true;
    if (pos.x < 0.){
        pos *= vec2(-1, 1);
        invCount++;
        fund = false;
    }
    if(pos.y < 0.){
        pos *= vec2(1, -1);
        invCount++;
        fund = false;
    }
    if(distance(pos, c1Pos) < r1 ){
        pos = circleInvert(pos, c1Pos, r1);
        invCount++;
        fund = false;
    }
    if(distance(pos, c2Pos) < r2 ){
        pos = circleInvert(pos, cPos2, r2);
        invCount++;
        fund = false;
    }
    if(fund)
        break;
}

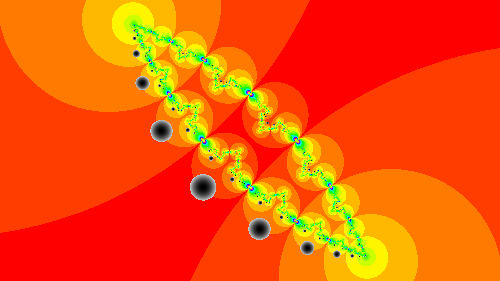
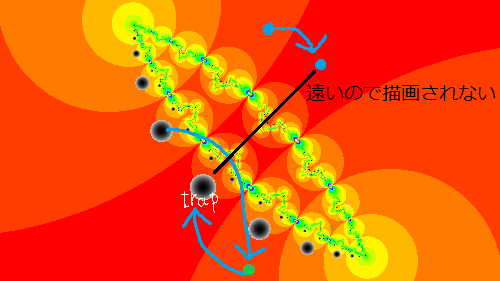
驚くことに，円板の内側の点は，内側の基本タイル(中央，右上の水色のタイル)に，外側の点は外側の基本タイル(右上の最も大きな紫色のタイル)に移されます．円板の内側のピクセルに対して計算を行うことで円板内の敷き詰めのみを描画することができますが，最終的な点の位置によって色付けを変えることで内側と外側を区別することもできます．
Hyperbolic TessellationはCPUベースで実装すると，計算量が多くなるため，端まで描画するのは大変なのですが，この方法を用いると端まできっちりとリアルタイムで描画することができ，GLSLの計算精度の限界まで拡大することができます．


敷き詰めの過程はこのような感じです．コードはこちら
Process of the Tessellation

Further Reading

• ポアンカレの円板モデル - Wikipedia
• 双曲幾何学 - Wikipedia
• 反転幾何学 - Wikipedia

Wikipediaの記事ですが，概要はつかめるのではないでしょうか．他には双曲幾何学への招待という教科書がお薦めですが，絶版となっています…

• Bulatov Abstract Creations - Math Projects
• Bending Circle Limits, Vladimir Bulatov

Hyperbolic Tessellationとその変形についてとても有益なスライドが公開されています.Bending Circle Limitsは円板を変形させてより面白いタイリングを描きます．一応実装には成功しましたが，完全に理解できていないので理解してまとめたいところです．

• The Conformal Hyperbolic Square and Its Ilk, Chamberlain Fong

円板を四角形に変形させる方法です．エッシャーの作品の中にも，円板を四角形にしようとする試みが見られる作品があります．

• Make Hyperbolic Tilings of Images

何種類かの双曲タイリングや画像のタイリングをみることができます．タイリングの条件についても少し記述されています．

おわりに

今回のGLSLで双曲タイリングを行うWebアプリケーションを作ったので試してみてください．対応しているパターンは２種類しかありませんが，タイリングの変形とWebカメラからの入力を敷き詰める機能を実装してあります．
Hyperbolic Tessellator
Shadertoyにもいくつかコードを上げています．

• Hyperbolic nyancat
• Hyperbolic triangular tiling 2
• Bending Circle
• Poincare Disk

数学の専門分野に入ってしまったうえ，説明もうまくできなかったのでわかりにくかったかもしれません．しかし，少し専門領域に踏み込むことで面白い題材が見つかるのではないでしょうか．明日の記事では今回触れた円に関する反転を用いたフラクタルについて紹介します．

GLSLで描くTessellation

qiita.com
GPUで暖を取りたい人のためのGLSL Advent Calendar 2016，23日目の記事です．

今回の記事ではGLSLで敷き詰め模様，Tessellationをレンダリングする方法を紹介します. これを読むような人ならばTessellationというと，ポリゴンの三角形分割を思い浮かべる方が多いかもしれませんがこの記事で話題にするのはより広義のTessellation,平面を平面図形で埋め合わせる平面充填のことです．タイリングとよんだりもします．GLSLでなんらかの絵を描いたことがある人ならば一度はチェッカーパターンを描いたことがあると思います．これも敷き詰め模様です．

正方形の敷き詰め

まず初めに，ごく簡単な正方形のtessellationを考えてみましょう．画像のように，正方形で平面全体を敷き詰めようとするとき，基本となる正方形を縦と横に動かすことを考えると思います．縦と横の平行移動，全４種類の変換の組み合わせで平面全体を正方形で埋め尽くすことができそうです．

GLSLで描画する場合はその逆を行います．すなわち，各ピクセルを敷き詰めを構成する４種類の変換で基本タイルに向かって動かしていきます．そうして，基本タイルに入ったあとで操作の回数によって色付けを行ったり，基本タイル上の色を参照するなどします．

以下が実装例です．Shadertoy上の実装です．

vec3 hsv2rgb(vec3 c){
    vec4 K = vec4(1.0, 2.0 / 3.0, 1.0 / 3.0, 3.0);
    vec3 p = abs(fract(c.xxx + K.xyz) * 6.0 - K.www);
    return c.z * mix(K.xxx, clamp(p - K.xxx, 0.0, 1.0), c.y);
}

const int MAX_ITERATIONS = 100;
void mainImage( out vec4 fragColor, in vec2 fragCoord )
{
    float ratio = iResolution.x / iResolution.y / 2.0;
    
    vec2 pos = (fragCoord.xy / iResolution.yy ) - vec2(ratio, 0.5);
    pos *= 10.;
    
    bool isFund = true;
    float opCount = 0.;
    float rectSize = 1.;

    for(int i = 0 ; i < MAX_ITERATIONS ; i++){
        isFund = true;
        if(pos.x < 0.){
            pos.x += rectSize;
            opCount++;
            isFund = false;
        }
        if(pos.x > rectSize){
            pos.x -= rectSize;
            opCount++;
            isFund = false;
        }
        if(pos.y < 0.){
            pos.y += rectSize;
            opCount++;
            isFund = false;
        }
        if(pos.y > rectSize){
            pos.y -= rectSize;
            opCount++;
            isFund = false;
        }
        if(isFund) break;
    }   
    fragColor = vec4(hsv2rgb(vec3(opCount * 0.2, 1., 1.)), 1.0 );
}

上の画像は操作の回数によって色をつけています．とても簡単で計算量の少なそうなコードになりました．各ピクセルを変換し続ける処理は，MAX_ITERATIONSによって制限せざるを得ませんが，多くの場合は問題ありません．

moduloによる効率化

多くの方はお気づきだと思いますが，単純な平行移動はmoduloをつかって効率化することができます．

if(pos.x < 0. || rectSize < pos.x){
    opCount += abs(floor(pos.x / rectSize));
    pos.x = mod(pos.x, rectSize);
    isFund = false;
}
if(pos.y < 0. || rectSize < pos.y){
    opCount += abs(floor(pos.y / rectSize));
    pos.y = mod(pos.y, rectSize);
    isFund = false;
}

操作の回数は商の絶対値をとってやれば計算できます．注意が必要なのは，基本タイルの位置が軸に沿っていない時です．正しく商と余りを計算するためには，タイルの辺が軸に沿うように一度平行移動や回転を行う必要があります．

正方形の敷き詰めを行うコードはShadertoyにアップロードしてあります．
https://www.shadertoy.com/view/4t3SDs

鏡映によるTessellation

もう一つ試してみましょう．

この模様はどのような基本タイルと変換で敷き詰めているでしょうか．平面は直角二等辺三角形でうめつくされています．また，よく見ると猫が三角形の各辺に対して鏡写しになっているのがわかります．これは三角形の各辺における鏡映変換という操作で移されています．基本としているタイルは(0, 0), (1, 0), (1, 0)を頂点に持つ赤い三角形です．この敷き詰めを描くコードの一部は以下のようになります．
x軸対称，y軸対称，そして斜辺による対称をとり続けることで基本タイルへと点を持っていくことができます．

for(int i = 0 ; i < MAX_ITERATIONS ; i++){
    isFund = true;
        
    if(pos.x < 0.){
        pos.x *= -1.;
        opCount++;
        isFund = false;
    }
    if(pos.y < 0.){
        pos.y *= -1.;
        opCount++;
        isFund = false;
    }
    // the inversion of line (x + y - 1 = 0)
    pos -= vec2(0, 1);
    pos = invRotateM * pos;
    if(pos.x > 0.){
        pos.x *= -1.;
        opCount++;
        isFund = false;
    }
    pos = rotateM * pos;
    pos += vec2(0, 1);
        
    if(isFund) break;
}

今回は，変換の回数で三角形の色を決めるのに加え，基本タイルの上に置いておいた猫のテクスチャを参照しています．完全なコードはこちらです．
https://www.shadertoy.com/view/4l3SDs

まとめ

今回紹介したアルゴリズムをまとめると以下のようになります．

1. 基本タイルを見つける．
2. 基本タイルを敷き詰めるための変換を見つける
3. 各ピクセルを基本タイルに入るまで変換し続ける
4. 変換の回数や，基本タイルの色を使って色をつける

Further Reading

• 装飾パターンの法則

最近知った本で，まだ読めてはいないのですが，敷き詰めパターンの分類や，それらを用いたデザインの方法が詳しく書かれています．こういったデザインの創作に興味のある方は必読ではないでしょうか．

• Hyperbolization of Euclidean Ornaments

ユークリッド平面上の敷き詰めを双曲平面上での敷き詰めに変形する手法について書かれています．また，今回紹介したアルゴリズムとほぼ同じものがReverse Pixel Lookupという名前で記述されています．この論文では既存の装飾パターンを読み込んで処理するということに主眼をおいています．
また，著者が書いたmorenamentsというソフトは敷き詰めの挙動を見るのに役に立つのではないかと思います．

おわりに

GLSLで敷き詰め模様をレンダリングするアルゴリズムを紹介しました．基本がわかれば色々と応用がきくと思います．明日の記事では双曲平面上でのタイルの敷き詰め，Hyperbolic Tessellationについて紹介します．

数学とアートのカンファレンス，Bridgesの紹介

www.adventar.org
この記事は日曜数学Adbent Calender7日目の記事です．今年の夏に8月9日から8月13日までフィンランドで開催されたBridgesというカンファレンスに参加してきました.今回はこの会議について紹介します．

Bridgesとは

Bridgesは数学とアートやその他の文化に関する国際会議です.
The Bridges Organization - About Bridges
Mathematics, Music, Art, Architecture, Education, Cultureの謳い文句の通り,数学だけではなく,数学とその他の文化的なものとの関わりを育てていくことを目的としています.参加者のバックグラウンドは数学者,教師,アーティスト,音楽家,パフォーマー,プログラマー等と多岐に渡り，学際的な領域にいる人々が集まります.このような領域の会議としては世界最大のものらしく，今年は350人ほどが参加したようです．
会では論文発表やワークショップの他，常設でアート作品展示がされます．展示された作品は投票によって賞が与えられます．また，Public Dayという一般に開かれた日も設けられており，劇や詩の朗読，ジャグリングなどのパフォーマンスが行われます．
その他にも，空いた場所に机をおいて作品販売を行っていたり，ロビーで音楽演奏，ダンスを始める人がいたりと，自由な雰囲気で，会議というよりは祭典という言葉がふさわしいかもしれません．

Call for Submissions

いくつか募集分野について紹介します．2016年12月6日現在，2017年のサイトはあまり準備が整っていないようなので，詳しく知りたい場合は去年のページを読むと良いです．
The Bridges Organization - Bridges 2016

Call for Papers

論文はRegular paperとShort paperが募集されます．それぞれきちんと査読されます．採択されるとRegular paperは３０分，Short paperは１５分のスロットが与えられてプレゼンを行うことになります．過去の論文は以下のリンクから全て読むことができます．様々なネタの宝庫です．
The Bridges Archive
僕はShort paperを出して参加しました．ある特定のフラクタルを高速に描画するためのアルゴリズムについて記述しました．

Art Exihibition

アート作品の展示です．作品は事前に審査されます．論文とは異なり,会場に来れなくても展示料金を払えば展示させてもらえるようなので,信頼できる人に作品を預けて展示してもらうこともできるらしいです.過去の作品はこちらで見ることができます.
2016 Bridges Conference | Mathematical Art Galleries
2015年に行われた展示の様子がアップロードされていました．
vimeo.com

Short Movie Festival

動画作品の募集です．集められた作品はPublic Dayに上映会が行われます．1~5分が望ましい長さとされていますが，厳密な制限はないようです．
2016 Bridges Conference Short Movie Festival | Mathematical Art Galleries

Student Travel Scholarship

海外で行われるカンファレンスですから，結構お金がかかります．学生参加者には奨学金があります．参加料と開催地までの距離に応じて最大1000$までが給付されます．給付の条件は何らかの論文や作品の提出,もしくは学生ボランティアに参加を申し出ることです.今回は僕も奨学金を出していただきました．

終わりに

数学とアートの国際カンファレンスであるBridgesについて紹介しました．来年はカナダのWaterlooで7月27日から31日まで開催されます．普段の活動をこういった学術的，国際的な場所で発表するのも良いのではないでしょうか．それぞれの分野の募集締め切りは2月初めから5月半ばの間に設定されているので確認してみてください．
www.youtube.com
僕も参加のために論文を書いている最中です．Art ExihibitionやShort Movie Festivalにも出したいところですが，あまり目処はたっていません…
それでは,来年の皆様の活動が実りの多きものになりますように.

日曜数学Advent Calendar8日目の記事はToshiki Takahashiさんによる，"ポリゴングラフと経済学"だそうです．

点列をCatmull Rom曲線を通してBezier曲線列に変換する

前回，レイトレーシングでBezier曲線を描画する方法を紹介しました．しかし，Bezier曲線そのままでは意図した図形を描画することは大変です．今回は，特定の点列を通るCatmull Rom曲線という曲線をBezier曲線に変換する方法を紹介します．
当初，B-spline曲線からBezier曲線に変換する，Boehm's algorithmを使用しようかと考えたのですが，設定等が複雑なことと，点列を必ず通る精密な図形を描きたかったため，点列を必ず通るという特性を持つ．Catmull Rom曲線を使うことにしました．

scheme(Gauche)による実装はこちら
scheme-raytrace/points.scm at master · soma-arc/scheme-raytrace · GitHub
Processingによる実装も公開している人がいました．
Mike's Processing code snippet repository
この方法と，前回紹介したBezier曲線をレイトレする手法を用いて描いた曲線がこちらです．

各種曲線の概要はこのサイトが詳しいです．
デジタル・フロンティア-Digital Frontier | DF TALK | スプライン曲線の話
また，変換を理解するにあたって，このサイトが非常に勉強になりました．
t-pot 『3次曲線』
これに従い，順に曲線を見ていくことで，自然と変換の方法がわかります．

Ferguson/Coons曲線

基本となる曲線です．三次曲線を表すため，始点と終点，初速度，最終速度の4種のパラメータを用います．これを用いた曲線の計算式はt-potにすべて載っていますが，ここではあまり重要でないので，記述しません．Bezier曲線もCatmull Rom曲線も，この曲線を元に速度の求め方を考えていきます．

Bezier曲線

Ferguson/Coons曲線において，速度を直接決めるのは割と面倒ですので，指定された制御点から，速度を求めてやるようにします．これが，三次のBezier曲線です．を始点，終点としたとき，速度を以下のようにして求めます．


３という係数がBezier曲線の次数ですね．速度が求められれば，Ferguson/Coons曲線の式が使えます．

Catmull Rom曲線

Catmull Rom曲線では，点列すべてを通る曲線を定めることができます．点列のセグメントの前後合わせて4つの点を合わせてパラメータを決めます．ある点における速度を前後の移動量を足し合わせたものにというパラメータをかけたものとします．この値は通常，0.5が使われるため，基本的には，移動量の平均値をとることになります．


ここで注意が必要なのが，点列における始点，終点です．始点，終点では速度を求めるために必要な点がないため，違う速度を使ってあげる必要があります．t-potでは，最初と最後の速度の平均速度を使うとしています．僕は面倒だったので，実装する際には，あらかじめ点を挿入しておいてある，と仮定して無視しました．
パラメータに関しては，このpdfで知りました．
https://www.cs.cmu.edu/~462/projects/assn2/assn2/catmullRom.pdf

点列からBezier曲線の制御点を求める

さて，Catmull Rom曲線と同じ挙動をとるBezier曲線の制御点を求めてみましょう．Bezier曲線とCarmull Rom曲線のは等しくなることを利用して，方程式を解きます．ベジェ曲線の制御点をとすると点列の四点，を用いて以下のように求まります．


先に述べたように，は普通0.5です．これで，点列のあるセグメントに関するBezier曲線の制御点を求めることができました．これを点列全体に関して行えば，Bezier曲線列を得ることができます．

おわり

点列をCatmull Rom曲線を用いてBezier曲線に変換する方法を紹介しました．この方法と前回の記事の内容をあわせることで，点列で表現される図形をレイトレで描画することができます．しかし，点列が多い図形だと曲線の数が増えて，どうしても時間がかかってしまいます．BVHなどを用いて効率よくレイとの交差計算を行わなければ，とても使えたものではないでしょう．
Bezier曲線といえば，内分点をとっていく導出しか知りませんでしたが，今回見たような意味づけは知らなかったので勉強になりました．

レイトレでベジェ曲線を描画する(Ray tracing for curves primitive)

レイトレーシングで曲線を描画する方法をまとめます．とりあえず3つほど見つけたのですが，今回はこちらの方法を実装してみました．

• Koji Nakamaru and Yoshio Ono, RAY TRACING FOR CURVES PRIMITIVE, WSCG 2002.

ベジェ曲線を直接幅を持ったリボンのようなものとして描く方法で,髪の毛などの細いものを描画するのに向いているそうです.
レンダリング結果はこのような感じになりました．


青い球の位置が制御点です．太くしすぎたため，少しがたつきがでています．
アルゴリズム自体は割と単純で，擬似コードも載っているので実装は簡単だと思いますが，その意味を考えると結構つっかかるところが多かったため，メモしておきます．

scheme(Gauche)で書いたソースコードはこちら．このパストレーサでは構造体をベクタで表現しているため，コードはかなり汚いです…
scheme-raytrace/bezier.scm at master · soma-arc/scheme-raytrace · GitHub
ベジェ曲線の接線や分割に関してはこちらのサイトを参考に実装しました．
ベジエ曲線について - s.h’s page

この論文でも紹介されている他の方法はこちら

• レイマーチングを用いて，generalized cylinderとして描画する方法

Sphere Tracing: A Geometric Method for the Antialiased Ray Tracing of Implicit Surfaces | Computer Graphics Illinois

• 連続した球の移動として描く方法

Ray tracing objects defined by sweeping a sphere

アルゴリズムの流れ

• 論文のアルゴリズムはz軸が高さ(Z-UP)になっていますが，僕が今回使ったパストレーサーはy軸が高さ(Y-UP)となっているので，処理を行う前に簡単な変換を行っておきます.
• あらかじめ指定されたベジェ曲線の幅からベジェ曲線の分割の深さを推定
• 全体に座標変換をかけ，原点がレイの原点，レイの方向がz軸正の方向になるように変換します．
• ベジェ曲線を分割
• 一定の領域内に入っている分割されたベジェ曲線のセグメントの中で，レイがベジェ曲線の内側に入っているものを見つける．
• その中からレイに最も近いものを見つける

最大分割数の推定

ベジェ曲線を分割していくことで，接触を判定していきますが，分割する前に，その分割数を描画する曲線の幅から推定します．これにはWang’s methodと呼ばれるものを使います．この式にはというパラメータがありますが，論文ではという値を提案しています．これは髪などを描画する際に有効な値のようで，太い曲線を描画するためには分割数が小さくて，先の画像のように正しい帯にならないようです．太い曲線を描く際には注意が必要です．

ベジェ曲線を変換する

次に，ベジェ曲線の制御点に変換行列をかけて，レイが原点中心，z軸方向となるように座標系を変換します．以下のような変換行列が提示されています．

(Oはレイの原点，lはレイの方向，)
d=0の時はの符号に応じたx軸に関する90°回転とするようです．

まず，レイの原点まで平行移動をかけ，レイの向きがｚ軸の正の方向を向くように変換してやる必要があります．向きの変換には，z方向がレイの向きである，以下のような正規直交基底を用いることで，そのような変換をかけることができます．

正規直交基底の求め方は以下のようになります．
まず，レイの方向をz方向とすることから，z軸のベクトルが決まります．

次に，x方向を考えますが，この時に，y軸方向は０とすることで，z軸方向のベクトルをXZ平面において90°回転して正規化することで作る事ができます．

最後のy方向のベクトルは，二つのベクトルに直交するという条件

から，

が求められます．

分割

曲線の幅を持った矩形を考え，曲線の矩形領域がその矩形にかぶっていれば，ベジェ曲線を分割するという操作を最大分割数に到達するまで繰り返します．ベジェ曲線は凸包性があり，全体を矩形で囲えるため，それを利用することで簡単に領域を見ることができます．

ベジェ曲線の分割は，パラメータが0.5の部分で分割していきます．分割が終わると，そこにはベジェ曲線の列ができることになります．
実装としては再帰関数になります．scheme実装は多値を返すようにしました．
関数の引数はcがベジェ曲線のセグメント，v0, vnがベジェ曲線全体を見たときのパラメータの値，tがレイとの距離です．

(converge
 (lambda (depth c v0 vn t)
   (let* ((b (g:bounding-box c 0 0))
          (b-min (g:aabb-min b))
          (b-max (g:aabb-max b)))
     (cond ((or (>= (v:z b-min) t) (<= (v:z b-max) 0.000001)
                (>= (v:x b-min) width1) (<= (v:x b-max) (- width1))
                (>= (v:y b-min) width1) (<= (v:y b-max) (- width1)))
            (values #f #f))
           ((< depth 0)
            ;; ...
            )
           (else (let*-values
                  (((vm) (/ (+ v0 vn) 2))
                   ((cl cr) (bezier-split c 0.5))
                   ((hit-left? nt-left) (converge (- depth 1) cl v0 vm t))
                   ((hit-right? nt-right) (converge (- depth 1) cr vm vn t)))
                  (if (and hit-left? (< nt-left t))
                      (set! t nt-left))
                  (if (and hit-right? (< nt-right t))
                      (set! t nt-right))
                  (values (or hit-left? hit-right?) t)))))))

ここで気になったのが，擬似コード上では，

return
 converge(depth,   cl,   v0,   vm,   t)
 ||   converge(depth,   cr,   vm,   vn,   t);

と表現されている部分です．多くのプログラムは，||演算子で先に評価された値がtrueとなった場合に，後の演算は評価されないように最適化されるはずです．しかし，そうなるとレイと最も近い場所を得ることができません．擬似コードの場合，そのような最適化を考えないのが前提となるのでしょうか…そのため，今回の実装ではorを使いませんでした．

位置を見る

分割後は，各ベジェ曲線に対して，レイ（原点）が現在見ている曲線の内側に入っているかを考えます．ある点Qが，正しい領域にいるときに，以下の式を満たすそうです．

(dPは接線，Pは制御点)
今回考えるべきなのは，レイの位置なので，Qは原点の０となります．
また，カーブが急な場合はこのままではうまく判定できないため，となる場合に接線の向きを反転してやります.
このプロセスのコードを抜き出すを以下のようになります．一つ注意が必要なのは，接線との内積を取る時は，XY平面上でとり，Zの値は無視する必要があるということです．ベジェ曲線の制御点は三次元上の点として扱ってきたので，そのままの内積をとってしまいがちです．

(let* ((dir (v:diff (bezier-cp c 3) (bezier-cp c 0)))
       (dp0 (bezier-tan-vec c 0))
       (dp0 (if (< (dot2d dir dp0) 0)
                (v:scale dp0 -1)
                dp0))
       (dpn #f)
       (w #f)
       (v #f)
       (p #f))
  (if (< (dot2d dp0 (v:scale (bezier-cp c 0) -1)) 0)
      (values #f #f) ;; return
      (begin
       (set! dpn (bezier-tan-vec c 1))
       (set! dpn (if (< (dot2d dir dpn) 0)
                     (v:scale dpn -1)
                     dpn))
       (if (< (dot2d dpn (bezier-cp c (- n 1))) 0)
           (values #f #f) ;; return
           ;; ...
           ))))

レイの位置のパラメータを求める

次に，レイの位置のベジェ曲線のパラメータを求めます．この時，考えるベジェ曲線は直線として考えます．この直線に，原点から垂線を引き，その交点の位置からベジェ曲線のパラメータを求めます．

論文で出されているパラメータ，

をというベクトルで書きかえると

となり，wが，正射影ベクトルの長さで，をw:(1-w)で分割するときのパラメータであることがわかります．
あとは，分割前のベジェ曲線全体のパラメータである，から，wで分割する値を求め，ベジェ曲線上の点を計算します．

ここでもう一つ気になる点があり，直観的にvはベジェ曲線全体で考えたときのパラメータとなるはずなのですが，論文の擬似コードでは，現在見ているベジェ曲線のセグメントにパラメータを与えて評価しています．逆に，全体のベジェ曲線でパラメータを評価すると正しく動きませんでした．また，十分短い線分ならば，わざわざこのようなパラメータを求める必要がない気もします．ここだけは意図が理解できませんでした．

レイとの近さを比較する

最後に，計算された点が，幅をはみ出ていないか等を確かめ，レイとの近さ，すなわちzの値を比較して返します．

(begin
 (set! w (+ (* (v:x dir) (v:x dir))
            (* (v:y dir) (v:y dir))))
 (if (= w 0)
     (values #f #f)
     (begin
      (set! w (/ (+ (* (v:x (bezier-cp c 0)) (v:x dir))
                    (* (v:y (bezier-cp c 0)) (v:y dir)))
                 (- w)))
      (set! w (clamp w 0 1))
      (set! v (+ (* v0 (- 1 w)) (* vn w)))
      (set! p (bezier-point c v))
      (if (or (>= (+ (* (v:x p) (v:x p))
                     (* (v:y p) (v:y p))) width2)
              (<= (v:z p) 0.0001)
              (< t (v:z p)))
          (values #f #f)
          (values #t (v:z p))))))

法線について

法線ベクトルに関しては，特に論文中で言及がなかったので，レイの向かってきた方向の逆をそのまま返してやりました．円柱だと考えて返すこともできるでしょうけれど，細いものだとそんなに変わりはないかもしれません.

おわり

少々つっかかるところもありましたが，レイトレ―シングを用いてベジェ曲線を描画する方法を紹介しました．ベジェ曲線を直接扱うのは少し面倒ですが，曲線が描けるようになると表現の幅も広がると思います．次は点列からベジェ曲線列を求める方法をまとめます．

Djangoのtemplate engineをstandaloneで使う

DjangoはPythonのWebアプリケーションフレームワークです．そのテンプレートエンジンのみを使いたいときの設定方法を調べてみたところ新旧様々な情報があり，苦労しましたのでまとめておきます．しかし，後から気づいたのですが，jinja2というテンプレートエンジンがDjangoライクな文法を提供しているようで，テンプレートエンジンのみを使う場合はこちらの方が良いかもしれません…
ちなみに，DjangoのテンプレートエンジンはdjulaというCommon Lisp実装も存在しています．

環境はpython 2.7.10, django1.9.6です．Django自体はpipを用いて，

pip install django==1.9.6

でインストール．もしくは，現時点ではGitHubからリポジトリをクローンしてきても動きました．

import django
from django.conf import settings
from django.template import Context, Template, loader

settings.configure(TEMPLATE_DEBUG=True,
                   TEMPLATES=[{"BACKEND":'django.template.backends.django.DjangoTemplates',
                               "DIRS":"./"}])
django.setup()

t = Template("My name is {{ name }}")
c = Context({"name":"foo"})

print(t.render(c))

t = loader.get_template("index.tmpl")
c = Context({"users":
                 [{"id":0, "name": "hoge"},
                  {"id":1, "name": "foo"}]
             })

print(t.render(c))

index.tmpl
{% for user in users %}
   {{ user.id }} ... {{ user.name }}
{% endfor %}

テンプレートエンジンのみを使うためにはsettings.configureで設定を記述した後に，django.setup()を呼び出す必要があります．BACKENDが使用するテンプレートエンジンの設定で，DIRSが，get_templateで読み込まれるテンプレートを置くディレクトリになるはずです．
ContextにはJSONを読み込んでそのまま流し込むこともできます．ただし，真偽値(True, False)はJSONの値としてそのまま書けないので注意が必要です．

Orbit trapを考える

マンデルブロ集合などでよく使われるカラーリングのアルゴリズムにOrbit trapと呼ばれる手法があります．以前から試してみたかったのですが，ようやくある程度理解でき，このような作品をつくることができました．

Kleinyan Cat at Shadertoy
今考えるとたいした事はないアルゴリズムだったのですが，割と理解するのに時間がかかったのでまとめておきます．やはり，実際に手で書いて試してみるのが大事ですね…

Orbit trapとマンデルブロ集合

マンデルブロ集合のようなフラクタルは，Escape-time Fractalとも呼ばれ，ある式を繰り返し計算していき，その計算結果の収束，発散をみることで描かれるフラクタルです．
マンデルブロ集合の計算の仕方を簡単にまとめると，複素平面上に格子点を取ってその座標を複素数Cとし，以下の漸化式を繰り返し計算します．

が無限大に発散しないものがマンデルブロ集合となります．また，となると無限大に発散することがわかっています．
複素平面上の複素数の積は点の回転，拡大，縮小，複素数の和は点の平行移動になりますので，複素平面上に点の軌道が描かれることがわかります．
この軌道上にtrapとなる図形などを設定しておき，そこからの距離や角度を保持して，これを用いてカラーリングを行います．

点を用いたOrbit trap

まずは最も簡単な点を用いたOrbit trapを見てみます．

private double getDistance(Complex c,
                           Complex point,
                           int maxIteration)
{        
    double distance = 1e20;
    Complex z = new Complex(0, 0);
        
    for(int i=0; i<maxIteration; i++)
    {
        //Perform Mandelbrot iteration
        z = z.multiply(z);
        z = z.add(c);
               
        //Set new distance dist = min( dist, |z-point| )
        Complex zMinusPoint = new Complex(z);
        zMinusPoint = zMinusPoint.subtract(point);
            
        double zMinusPointModulus = zMinusPoint.magnitude();
        if(zMinusPointModulus < distance)
            distance = zMinusPointModulus;
    }
        
    return distance;
}

Orbit trap - Wikipedia, the free encyclopedia

レンダリング結果は載っていませんが，アルゴリズムの概要をWikipediaから引用しました．こうしてみると単純ですね．点を用いたOrbit trapで，あらかじめ設定した点と最も近い時の距離を用いてレンダリングを色を決定します．これとほぼ同じアルゴリズムで(-0.5, 2.0)の点でトラップし，distanceをそのままプロットしたのが以下の画像です．この画像はShadertoyのMandelbrot - orbit trapsを少し変更して生成したものです．

黒い点が連なっています．マンデルブロ集合では点の軌道がわかりにくく，点が連なる理由が見えてきません．個人的になれている接触ショットキー群でも考えてみたいと思います．

Orbit trapと接触ショットキー群

４つの円で構成される接触ショットキー群を考えます．この画像は，マンデルブロ集合と同じように，複素平面上に格子点を取り，その座標が４つの基本となる円盤に載っていた場合にその円に関する鏡映反転を行う，という操作を点がすべての円の外に出るまで繰り返し，その繰り返した回数に応じて色を塗った画像です．この点にも軌道ができますので，Orbit trapを行うことができます．
Kleinyan Catの191行目あたりのコメントアウトを外してCompileし直すと，次のような画像が得られます．

    vec3 hsv = hsv2rgb(vec3(0.04 * loopNum,1.0,1.0));
   
    col.xyz = mix( hsv, col.xyz, col.w );
    fragColor = col;
 
    if(trap1/1000. < 0.8){
    	fragColor = vec4(vec3(trap1/1000.), 1.0);
    }else{
    	fragColor = vec4( hsv, 1.0);
    }

これはt1c = vec2(-100, -100)と軌道の点が最も近い時の距離を保持し，スケーリングしてプロットしたものです．パラメータが動いても動かない点がありますが，これが最初に設定した点(-100, -100)です．
二つの円盤に点がかぶってしまっているのであまりよくない画像ですが，この図形の点の大体の軌道を考えてみるとこんな感じになると思います．

それぞれの点は反転を行うと，円の中心から点の方向に，円盤ひとつずつ降りていくような挙動を取ります．トラップする点，t1cを弄ってみるとより点列ができる理由がわかりやすいかもしれません．
ちなみにこの図形は二つの領域に円の極限（極限集合）で分けられており，この内側の点は内側に，外側の点は必ず外側に移るようになっています．つまり，内側にトラップする点を置いておくと，点列は内側にしか現れません．t1cを(0, 0)に置いてみるとよくわかります．

Orbit trapを用いたカラーリング

アルゴリズムは案外単純であることがわかりましたが，果たしてこれで面白いカラーリングができるのでしょうか…iq先生のMandelbrot - orbit trapsでは点との距離を見るトラップとaverage trap distance to lineというトラップを行い，それらをうまく変換しているようです．ズームや，経過時間に応じてトラップする点をずらすなど，色々とうまくやっているようで，使いこなすには経験とセンスが必要な気がします…定石などがあるのでしょうか．
今回はlineに関するtrapは試していませんが，64行目あたりの

col += 2.0*sqrt(c1*col1*col2);

を

col += c2;

にすると大体の挙動がわかります．

Bitmap Orbit traps

さて，次にtrapに画像を用いるBitmap Orbit trapを行ってみたいと思います．こちらは絵を移していくものなので，普通に色付けするよりは簡単に面白いものができるのではないかと思います．Bitmap Orbit trapの実装はFractal Nyancatが参考になります．Kleinyan Catのトラップの処理は以下のようになります．

if (col.w < 0.1)
	col = getNyanCatColor( pos - cPos[0] * scale);
if (col.w < 0.1)
	col = getNyanCatColor( pos - cPos[1] * scale);
if (col.w < 0.1)
	col = getNyanCatColor( pos - cPos[2] * scale);
if (col.w < 0.1)
	col = getNyanCatColor( pos - cPos[3] * scale);

cPos * scaleがトラップする点です．点の位置から引くことで画像の始点からの位置を求めています．画像は原点から四円の中心への直線の延長直線状に置いています．絵がない部分には，透明度が設定されているので，絵が取得されていれば画素値は取得されないようになっています．
getNyanCatColorという関数は，Fractal Nyancatで使われているものを整えました．

vec4 getNyanCatColor( vec2 p ){
	p += vec2(100, 100);//offset
	p = p / 200.;
	p = clamp(p,0.0,1.0);
	p.x = p.x*40.0/256.0;
	float fr = floor( mod( 20.0*iGlobalTime, 6.0 ) );
	p.x += fr*40.0/256.0;
	return texture2D( iChannel0, p);
}

トラップに使用する点の中心に画像を置きたいので，適当に移動した後にスケーリングします．ここら辺は実験的に決めましたが，ちゃんと考えれば一般的な解はあるはずです．
clampすることで，0以下は0に，1以上は1に丸まられ，画像から離れすぎた場所は角の画素が参照されることになります．こうすることで，パフォーマンスに影響がでる条件分岐を削る事もできます．参照しているテクスチャは6フレームの猫が収められているので，うまく参照してやります．トラップに用いる最初の猫の位置はこのような感じです．(フレームの外側に2体隠れていて，合計4体描かれているはずです．)

点の軌道上に，最初に置いた猫の画像があれば，そこから画素値を取得し，その色を取得する感じです．結果としてこのような画像が得られました．

移された猫は隣り合う円盤同士で鏡写しになり，歪みが入っているのがわかるでしょうか．これが円に関する鏡映変換の作用です．また，この結果はクライン群を生成する４つの生成元で一つの画像を写していくことと同じようです．以前描いた以下のようなものが大元となる一体の蝶を4つの生成元で移したものです．
GitHub - soma-arc/KleinianWalker: Draw limit set of Kleinian group and orbit of figure

生成元で直接移していくためには，生成元の組み合わせの木構造を幅優先で探索していかなければならないのですが，探索が深くなるにつれて，指数オーダーで計算量が増えていくので，細かく描こうとするほど時間がかかります．Bitmap Orbit trapが使えれば，そのような探索が必要でなくなり，高速な描画ができるということになります．

おわりに

今回は点と画像を用いたOrbit trapのみを試しましたが，他の種類のものも試す必要がありますね．また，Bitmap Orbit trapを用いることである画像を生成元で移していくような作品も高速に描画できることがわかりました．このようなテクニックはまだまだあるようで，一つ一つ実際に実装して理解していく必要がありそうです．日々精進あるのみですね．

Reference

1. Orbit trap - Wikipedia, the free encyclopedia
2. geometric orbit traps by Inigo Quilez
3. bitmap orbit traps by Inigo Quilez
4. Mandelbrot - orbit traps by iq
5. Fractal Nyancat by iq
6. Make Fractals of Images