レイトレでベジェ曲線を描画する(Ray tracing for curves primitive)

レイトレーシングで曲線を描画する方法をまとめます．とりあえず3つほど見つけたのですが，今回はこちらの方法を実装してみました．

Koji Nakamaru and Yoshio Ono, RAY TRACING FOR CURVES PRIMITIVE, WSCG 2002.

ベジェ曲線を直接幅を持ったリボンのようなものとして描く方法で,髪の毛などの細いものを描画するのに向いているそうです.
レンダリング結果はこのような感じになりました．
f:id:soma_arc:20160504163335p:plain
f:id:soma_arc:20160504163401p:plain
青い球の位置が制御点です．太くしすぎたため，少しがたつきがでています．
アルゴリズム自体は割と単純で，擬似コードも載っているので実装は簡単だと思いますが，その意味を考えると結構つっかかるところが多かったため，メモしておきます．

scheme(Gauche)で書いたソースコードはこちら．このパストレーサでは構造体をベクタで表現しているため，コードはかなり汚いです…
scheme-raytrace/bezier.scm at master · soma-arc/scheme-raytrace · GitHub
ベジェ曲線の接線や分割に関してはこちらのサイトを参考に実装しました．
ベジエ曲線について - s.h’s page

この論文でも紹介されている他の方法はこちら

レイマーチングを用いて，generalized cylinderとして描画する方法

Sphere Tracing: A Geometric Method for the Antialiased Ray Tracing of Implicit Surfaces | Computer Graphics Illinois

連続した球の移動として描く方法

Ray tracing objects defined by sweeping a sphere

アルゴリズムの流れ

論文のアルゴリズムはz軸が高さ(Z-UP)になっていますが，僕が今回使ったパストレーサーはy軸が高さ(Y-UP)となっているので，処理を行う前に簡単な変換を行っておきます.
あらかじめ指定されたベジェ曲線の幅からベジェ曲線の分割の深さを推定
全体に座標変換をかけ，原点がレイの原点，レイの方向がz軸正の方向になるように変換します．
ベジェ曲線を分割
一定の領域内に入っている分割されたベジェ曲線のセグメントの中で，レイがベジェ曲線の内側に入っているものを見つける．
その中からレイに最も近いものを見つける

最大分割数の推定

ベジェ曲線を分割していくことで，接触を判定していきますが，分割する前に，その分割数を描画する曲線の幅から推定します．これにはWang’s methodと呼ばれるものを使います．この式には ${\epsilon}$ というパラメータがありますが，論文では ${\epsilon = width /20}$ という値を提案しています．これは髪などを描画する際に有効な値のようで，太い曲線を描画するためには分割数が小さくて，先の画像のように正しい帯にならないようです．太い曲線を描く際には注意が必要です．

ベジェ曲線を変換する

次に，ベジェ曲線の制御点に変換行列をかけて，レイが原点中心，z軸方向となるように座標系を変換します．以下のような変換行列が提示されています．
${\left( \begin{array}{cccc} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\-o_x & -o_y & -o_z & 1 \end{array} \right) \left( \begin{array}{cccc} l_z/d & -l_xl_y/d & l_x & 0 \\ 0 & d & l_y & 0 \\-l_x/d & -l_yl_z/d & l_z & 0 \\ 0 & 0 & 0 & 1 \end{array} \right)}$
(Oはレイの原点，lはレイの方向， ${d = \sqrt{l_x^2 + l_x^2}}$ )
d=0の時は ${l_y}$ の符号に応じたx軸に関する90°回転とするようです．

まず，レイの原点まで平行移動をかけ，レイの向きがｚ軸の正の方向を向くように変換してやる必要があります．向きの変換には，z方向がレイの向きである，以下のような正規直交基底 ${(e_x, e_y, e_z)}$ を用いることで，そのような変換をかけることができます．
f:id:soma_arc:20160526174719j:plain
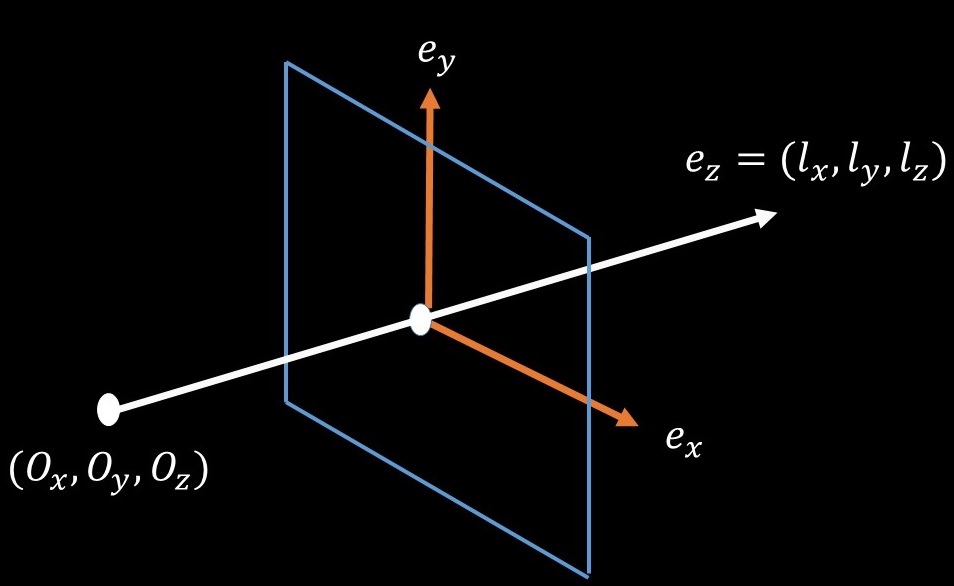
正規直交基底の求め方は以下のようになります．
まず，レイの方向をz方向とすることから，z軸のベクトルが決まります．
${e_z = \left( \begin{array}{c} l_x \\ l_y \\ l_z \end{array} \right) }$
次に，x方向を考えますが，この時に，y軸方向は０とすることで，z軸方向のベクトルをXZ平面において90°回転して正規化することで作る事ができます．
${e_x = \left( \begin{array}{c} l_z/d \\ 0 \\l_x/d \end{array} \right) }$
最後のy方向のベクトルは，二つのベクトルに直交するという条件
${e_x \cdot e_y = 0\ \& \ e_z \cdot e_y = 0}$
から，
${e_y = \left( \begin{array} {c}-l_xl_y/d \\ d \\-l_yl_z/d \end{array} \right) }$
が求められます．

分割

曲線の幅を持った矩形を考え，曲線の矩形領域がその矩形にかぶっていれば，ベジェ曲線を分割するという操作を最大分割数に到達するまで繰り返します．ベジェ曲線は凸包性があり，全体を矩形で囲えるため，それを利用することで簡単に領域を見ることができます．

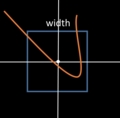
ベジェ曲線の分割は，パラメータが0.5の部分で分割していきます．分割が終わると，そこにはベジェ曲線の列ができることになります．
実装としては再帰関数になります．scheme実装は多値を返すようにしました．
関数の引数はcがベジェ曲線のセグメント，v0, vnがベジェ曲線全体を見たときのパラメータの値，tがレイとの距離です．

(converge
 (lambda (depth c v0 vn t)
   (let* ((b (g:bounding-box c 0 0))
          (b-min (g:aabb-min b))
          (b-max (g:aabb-max b)))
     (cond ((or (>= (v:z b-min) t) (<= (v:z b-max) 0.000001)
                (>= (v:x b-min) width1) (<= (v:x b-max) (- width1))
                (>= (v:y b-min) width1) (<= (v:y b-max) (- width1)))
            (values #f #f))
           ((< depth 0)
            ;; ...
            )
           (else (let*-values
                  (((vm) (/ (+ v0 vn) 2))
                   ((cl cr) (bezier-split c 0.5))
                   ((hit-left? nt-left) (converge (- depth 1) cl v0 vm t))
                   ((hit-right? nt-right) (converge (- depth 1) cr vm vn t)))
                  (if (and hit-left? (< nt-left t))
                      (set! t nt-left))
                  (if (and hit-right? (< nt-right t))
                      (set! t nt-right))
                  (values (or hit-left? hit-right?) t)))))))

ここで気になったのが，擬似コード上では，

return
 converge(depth,   cl,   v0,   vm,   t)
 ||   converge(depth,   cr,   vm,   vn,   t);

と表現されている部分です．多くのプログラムは，||演算子で先に評価された値がtrueとなった場合に，後の演算は評価されないように最適化されるはずです．しかし，そうなるとレイと最も近い場所を得ることができません．擬似コードの場合，そのような最適化を考えないのが前提となるのでしょうか…そのため，今回の実装ではorを使いませんでした．

位置を見る

分割後は，各ベジェ曲線に対して，レイ（原点）が現在見ている曲線の内側に入っているかを考えます．ある点Qが，正しい領域にいるときに，以下の式を満たすそうです．
${ dP_0 \cdot (Q - P_0) \geq 0 \ \&\ dP_n \cdot (P_n - Q) \geq 0 }$
(dPは接線，Pは制御点)
今回考えるべきなのは，レイの位置なので，Qは原点の０となります．
また，カーブが急な場合はこのままではうまく判定できないため， ${ dP_* \cdot (P_n - P_0) < 0 }$ となる場合に接線 ${dP_*}$ の向きを反転してやります.
このプロセスのコードを抜き出すを以下のようになります．一つ注意が必要なのは，接線との内積を取る時は，XY平面上でとり，Zの値は無視する必要があるということです．ベジェ曲線の制御点は三次元上の点として扱ってきたので，そのままの内積をとってしまいがちです．

(let* ((dir (v:diff (bezier-cp c 3) (bezier-cp c 0)))
       (dp0 (bezier-tan-vec c 0))
       (dp0 (if (< (dot2d dir dp0) 0)
                (v:scale dp0 -1)
                dp0))
       (dpn #f)
       (w #f)
       (v #f)
       (p #f))
  (if (< (dot2d dp0 (v:scale (bezier-cp c 0) -1)) 0)
      (values #f #f) ;; return
      (begin
       (set! dpn (bezier-tan-vec c 1))
       (set! dpn (if (< (dot2d dir dpn) 0)
                     (v:scale dpn -1)
                     dpn))
       (if (< (dot2d dpn (bezier-cp c (- n 1))) 0)
           (values #f #f) ;; return
           ;; ...
           ))))

レイの位置のパラメータを求める

次に，レイの位置のベジェ曲線のパラメータを求めます．この時，考えるベジェ曲線は直線として考えます．この直線に，原点から垂線を引き，その交点の位置からベジェ曲線のパラメータを求めます．

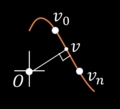
論文で出されているパラメータ，
${ w = \frac{x_0(x_n - x_0)+y_0(y_n - y_0)}{(x_n - x_0)^2+(y_n - y_0)^2} }$
を ${(x_0, y_0) = p_0,\ (x_n, y_n) = p_n}$ というベクトルで書きかえると
${ w = \frac{\vec{p_0} \cdot (\vec{p_n} - \vec{p_0})}{|\vec{p_n} - \vec{p_0}|^2} }$
となり，wが，正射影ベクトルの長さで， ${\vec{p_n} - \vec{p_0}}$ をw:(1-w)で分割するときのパラメータであることがわかります．
あとは，分割前のベジェ曲線全体のパラメータである， ${v_0, v_n}$ から，wで分割する値を求め，ベジェ曲線上の点を計算します．
${ v = v_0(1 - w) + v_n w }$
ここでもう一つ気になる点があり，直観的にvはベジェ曲線全体で考えたときのパラメータとなるはずなのですが，論文の擬似コードでは，現在見ているベジェ曲線のセグメントにパラメータを与えて評価しています．逆に，全体のベジェ曲線でパラメータを評価すると正しく動きませんでした．また，十分短い線分ならば，わざわざこのようなパラメータを求める必要がない気もします．ここだけは意図が理解できませんでした．

レイとの近さを比較する

最後に，計算された点が，幅をはみ出ていないか等を確かめ，レイとの近さ，すなわちzの値を比較して返します．

(begin
 (set! w (+ (* (v:x dir) (v:x dir))
            (* (v:y dir) (v:y dir))))
 (if (= w 0)
     (values #f #f)
     (begin
      (set! w (/ (+ (* (v:x (bezier-cp c 0)) (v:x dir))
                    (* (v:y (bezier-cp c 0)) (v:y dir)))
                 (- w)))
      (set! w (clamp w 0 1))
      (set! v (+ (* v0 (- 1 w)) (* vn w)))
      (set! p (bezier-point c v))
      (if (or (>= (+ (* (v:x p) (v:x p))
                     (* (v:y p) (v:y p))) width2)
              (<= (v:z p) 0.0001)
              (< t (v:z p)))
          (values #f #f)
          (values #t (v:z p))))))

法線について

法線ベクトルに関しては，特に論文中で言及がなかったので，レイの向かってきた方向の逆をそのまま返してやりました．円柱だと考えて返すこともできるでしょうけれど，細いものだとそんなに変わりはないかもしれません.

おわり

少々つっかかるところもありましたが，レイトレ―シングを用いてベジェ曲線を描画する方法を紹介しました．ベジェ曲線を直接扱うのは少し面倒ですが，曲線が描けるようになると表現の幅も広がると思います．次は点列からベジェ曲線列を求める方法をまとめます．
f:id:soma_arc:20160526164840p:plain