前回,レイトレーシングでBezier曲線を描画する方法を紹介しました.しかし,Bezier曲線そのままでは意図した図形を描画することは大変です.今回は,特定の点列を通るCatmull Rom曲線という曲線をBezier曲線に変換する方法を紹介します.
当初,B-spline曲線からBezier曲線に変換する,Boehm's algorithmを使用しようかと考えたのですが,設定等が複雑なことと,点列を必ず通る精密な図形を描きたかったため,点列を必ず通るという特性を持つ.Catmull Rom曲線を使うことにしました.
scheme(Gauche)による実装はこちら
scheme-raytrace/points.scm at master · soma-arc/scheme-raytrace · GitHub
Processingによる実装も公開している人がいました.
Mike's Processing code snippet repository
この方法と,前回紹介したBezier曲線をレイトレする手法を用いて描いた曲線がこちらです.

各種曲線の概要はこのサイトが詳しいです.
デジタル・フロンティア-Digital Frontier | DF TALK | スプライン曲線の話
また,変換を理解するにあたって,このサイトが非常に勉強になりました.
t-pot 『3次曲線』
これに従い,順に曲線を見ていくことで,自然と変換の方法がわかります.
Ferguson/Coons曲線

基本となる曲線です.三次曲線を表すため,始点と終点,初速度,最終速度の4種のパラメータを用います.これを用いた曲線の計算式はt-potにすべて載っていますが,ここではあまり重要でないので,記述しません.Bezier曲線もCatmull Rom曲線も,この曲線を元に速度の求め方を考えていきます.
Bezier曲線
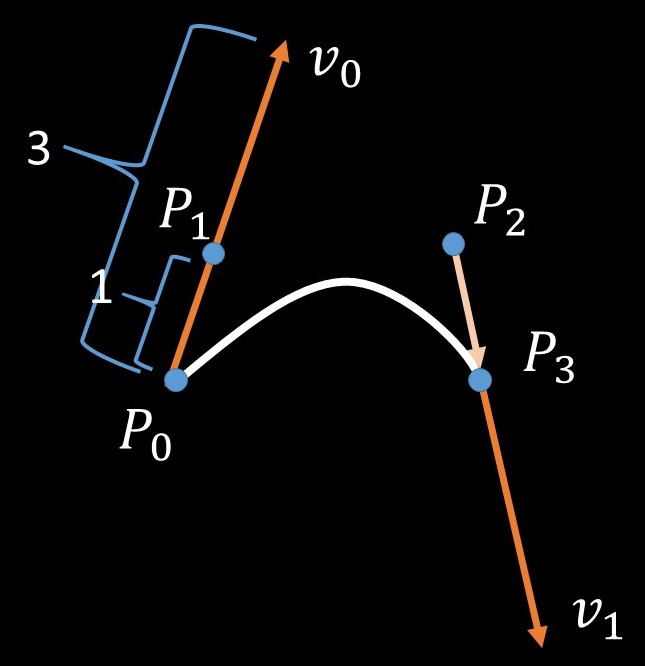
Ferguson/Coons曲線において,速度を直接決めるのは割と面倒ですので,指定された制御点から,速度を求めてやるようにします.これが,三次のBezier曲線です.を始点,終点としたとき,速度
を以下のようにして求めます.
3という係数がBezier曲線の次数ですね.速度が求められれば,Ferguson/Coons曲線の式が使えます.
Catmull Rom曲線
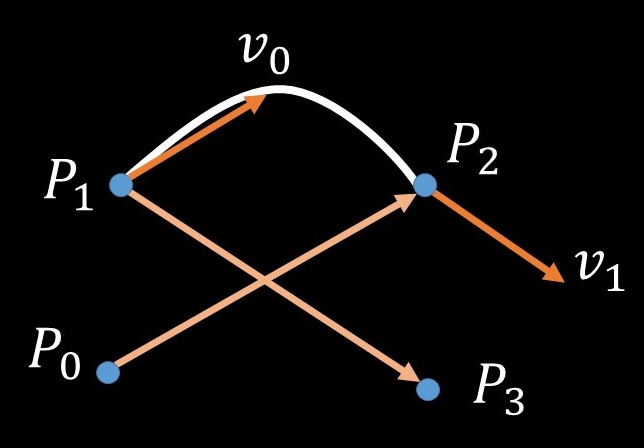
Catmull Rom曲線では,点列すべてを通る曲線を定めることができます.点列のセグメントの前後合わせて4つの点を合わせてパラメータを決めます.ある点における速度を前後の移動量を足し合わせたものにというパラメータをかけたものとします.この値は通常,0.5が使われるため,基本的には,移動量の平均値をとることになります.
ここで注意が必要なのが,点列における始点,終点です.始点,終点では速度を求めるために必要な点がないため,違う速度を使ってあげる必要があります.t-potでは,最初と最後の速度の平均速度を使うとしています.僕は面倒だったので,実装する際には,あらかじめ点を挿入しておいてある,と仮定して無視しました.
パラメータに関しては,このpdfで知りました.
https://www.cs.cmu.edu/~462/projects/assn2/assn2/catmullRom.pdf
点列からBezier曲線の制御点を求める
さて,Catmull Rom曲線と同じ挙動をとるBezier曲線の制御点を求めてみましょう.Bezier曲線とCarmull Rom曲線のは等しくなることを利用して,方程式を解きます.ベジェ曲線の制御点を
とすると点列の四点,
を用いて以下のように求まります.
先に述べたように,は普通0.5です.これで,点列のあるセグメントに関するBezier曲線の制御点を求めることができました.これを点列全体に関して行えば,Bezier曲線列を得ることができます.
おわり
点列をCatmull Rom曲線を用いてBezier曲線に変換する方法を紹介しました.この方法と前回の記事の内容をあわせることで,点列で表現される図形をレイトレで描画することができます.しかし,点列が多い図形だと曲線の数が増えて,どうしても時間がかかってしまいます.BVHなどを用いて効率よくレイとの交差計算を行わなければ,とても使えたものではないでしょう.
Bezier曲線といえば,内分点をとっていく導出しか知りませんでしたが,今回見たような意味づけは知らなかったので勉強になりました.